Introduction to Quadratic Functions
In the realm of mathematics, quadratic functions play a pivotal role, offering insights into various real-world phenomena and serving as fundamental building blocks for higher-level concepts. A quadratic function is a polynomial function of degree two, expressed in the form
�(�)=��2+��+�
f(x)=ax
2
+bx+c, where
�
a,
�
b, and
�
c are constants, and
�
a is not equal to zero. Understanding these functions is crucial for students and professionals alike, as they are extensively utilized in fields ranging from physics and engineering to economics and computer science.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of degree two. The standard form of a quadratic equation is
��2+��+�=0
ax
2
+bx+c=0, where
�
a,
�
b, and
�
c are constants, and
�
a is not equal to zero. Quadratic equations are characterized by the presence of a squared term (
�2
x
2
), and they can have either real or complex roots. The discriminant (
�2−4��
b
2
−4ac) determines the nature of the roots: positive discriminant indicates two real roots, zero discriminant indicates repeated real roots, and negative discriminant indicates complex roots.
Graphical Representation
Graphically, quadratic functions form a parabolic curve when plotted on a Cartesian plane. The shape and position of the parabola are determined by the coefficients
�
a,
�
b, and
�
c in the quadratic equation. The vertex of the parabola represents the minimum or maximum point of the function, depending on the direction of the opening. The axis of symmetry is a vertical line passing through the vertex, dividing the parabola into two symmetrical halves. The x-intercepts correspond to the solutions of the quadratic equation, while the y-intercept represents the value of the function when
�=0
x=0.
Transformations of Quadratic Functions
Manipulating the parameters
�
a,
�
b, and
�
c in the quadratic equation leads to various transformations of the corresponding quadratic function. Changing the value of
�
a affects the width and direction of the parabola, with
∣�∣
∣a∣ determining the degree of stretching or compression along the y-axis. The parameter
�
b controls the horizontal shift of the parabola (translation), while
�
c determines the vertical shift. Negative values of
�
a and
�
b cause reflections across the x-axis and y-axis, respectively.
Optimization Problems
Quadratic functions are often employed in optimization problems, where the goal is to maximize or minimize a certain quantity. For instance, in economics, quadratic functions can model cost, revenue, and profit functions, allowing businesses to determine the optimal level of production or pricing. Similarly, in engineering and physics, quadratic functions describe various phenomena such as projectile motion, where the objective is to maximize the range or height of the projectile.
Solving Quadratic Equations
Several methods exist for solving quadratic equations, including factoring, completing the square, and using the quadratic formula. Factoring involves expressing the quadratic equation as a product of linear factors, facilitating the identification of its roots. Completing the square transforms the quadratic equation into a perfect square trinomial, enabling the extraction of its roots. The quadratic formula provides a direct formulaic approach to finding the roots of any quadratic equation, regardless of its coefficients.
Graphical Solutions
In addition to algebraic methods, quadratic equations can be solved graphically by finding the points of intersection between the quadratic curve and other functions or lines. This approach offers a geometric interpretation of the solutions and can be particularly useful in visualizing complex equations involving multiple variables. Graphing calculators and computer software make this process more accessible, allowing for efficient and accurate solutions to quadratic equations.
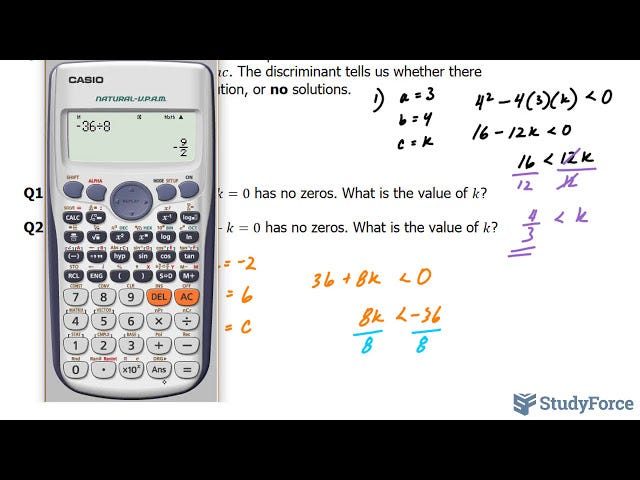
Practical Tips for Using Calculators
When dealing with quadratic functions, modern technology can significantly aid in computations and problem-solving. Graphing calculators equipped with advanced functionality enable users to visualize quadratic functions, plot graphs, and analyze key features such as vertex, intercepts, and symmetry. Leveraging these tools can streamline the learning process and enhance understanding of quadratic concepts, especially for visual learners.
Common Mistakes to Avoid
Despite their utility, quadratic functions can pose challenges for students, leading to common mistakes and misconceptions. One such pitfall is misinterpreting the graphical representation of quadratic equations, particularly in distinguishing between minimum and maximum points. Additionally, errors in algebraic manipulation, such as incorrect substitution or simplification, can result in inaccurate solutions. Vigilance and practice are essential in overcoming these obstacles.
Real-life Examples and Applications
The applicability of quadratic functions extends far beyond the confines of the classroom, manifesting in various real-life scenarios. For example, in physics, quadratic equations govern the trajectory of projectiles, guiding the design of artillery and missiles. In economics, quadratic models describe the relationship between cost, revenue, and profit, aiding businesses in optimizing their operations. By exploring these examples, learners gain a deeper appreciation for the practical significance of quadratic functions.
Advanced Techniques and Extensions
Beyond the fundamental concepts, quadratic functions offer avenues for exploration and extension into more advanced topics. Quadratic regression analysis, for instance, involves fitting quadratic models to empirical data, enabling predictive modeling and trend analysis. Quadratic inequalities extend the notion of quadratic equations to include regions of inequality, opening new possibilities for optimization and constraint satisfaction.
Exploring Related Concepts
Quadratic functions are part of a broader family of polynomial functions, which include cubic, quartic, and higher-degree polynomials. Understanding the connections between these functions and their properties deepens one’s grasp of algebraic concepts and enhances problem-solving abilities. Polynomial long division provides a systematic method for dividing polynomials, facilitating the manipulation and analysis of polynomial expressions.
Challenges and Practice Exercises
To master the intricacies of quadratic functions, students are encouraged to engage in challenging exercises and problem-solving tasks. Practice questions covering various aspects of quadratic equations, functions, and applications allow for the consolidation of knowledge and the development of problem-solving skills. By tackling diverse problems and seeking assistance when needed, learners can overcome obstacles and achieve proficiency in quadratic mathematics.
Resources for Further Learning
For those seeking to delve deeper into the realm of quadratic functions, a wealth of resources is available both online and in print. Educational websites offer tutorials, interactive lessons, and practice problems tailored to different learning styles and levels of proficiency. Additionally, textbooks and academic journals provide comprehensive coverage of quadratic concepts, accompanied by examples, explanations, and exercises for self-assessment.
Conclusion
In conclusion, navigating quadratic functions entails mastering fundamental concepts, leveraging technological tools, and exploring real-life applications. By understanding the structure and behavior of quadratic equations and functions, individuals can solve problems, make informed decisions, and appreciate the beauty of mathematical abstraction. Through practice, perseverance, and a curious mindset, anyone can unlock the potential of quadratic mathematics and embark on a journey of discovery and learning.